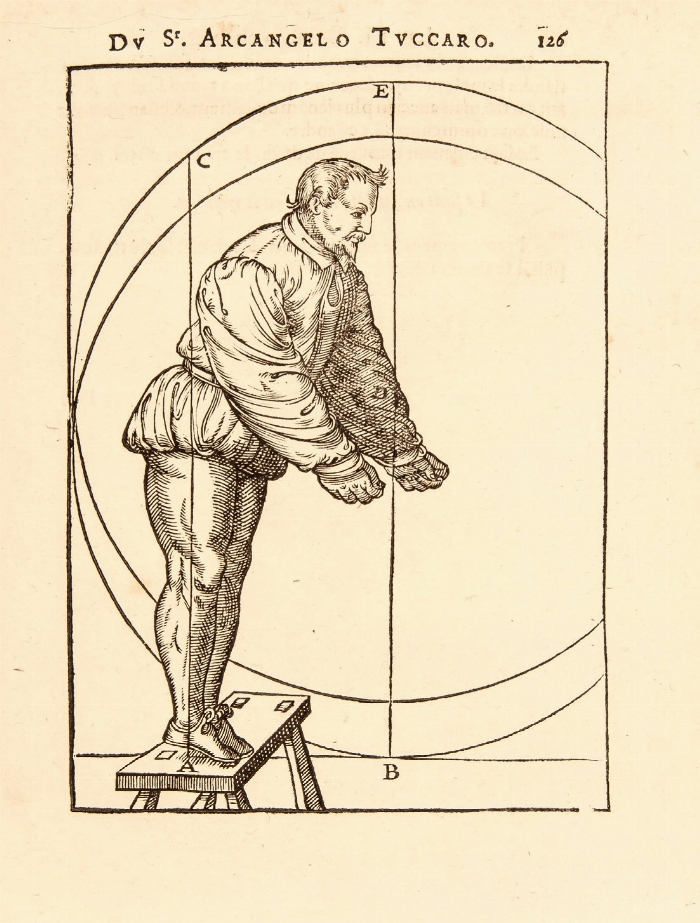
-
 10th April 2024Rare Books, Prints, Autograph and Documents.Lot 151. WOOD. Les Ruines de Palmyre, autrement dite Tedmor, au Desert. Londres, A. Millar,
10th April 2024Rare Books, Prints, Autograph and Documents.Lot 151. WOOD. Les Ruines de Palmyre, autrement dite Tedmor, au Desert. Londres, A. Millar, -
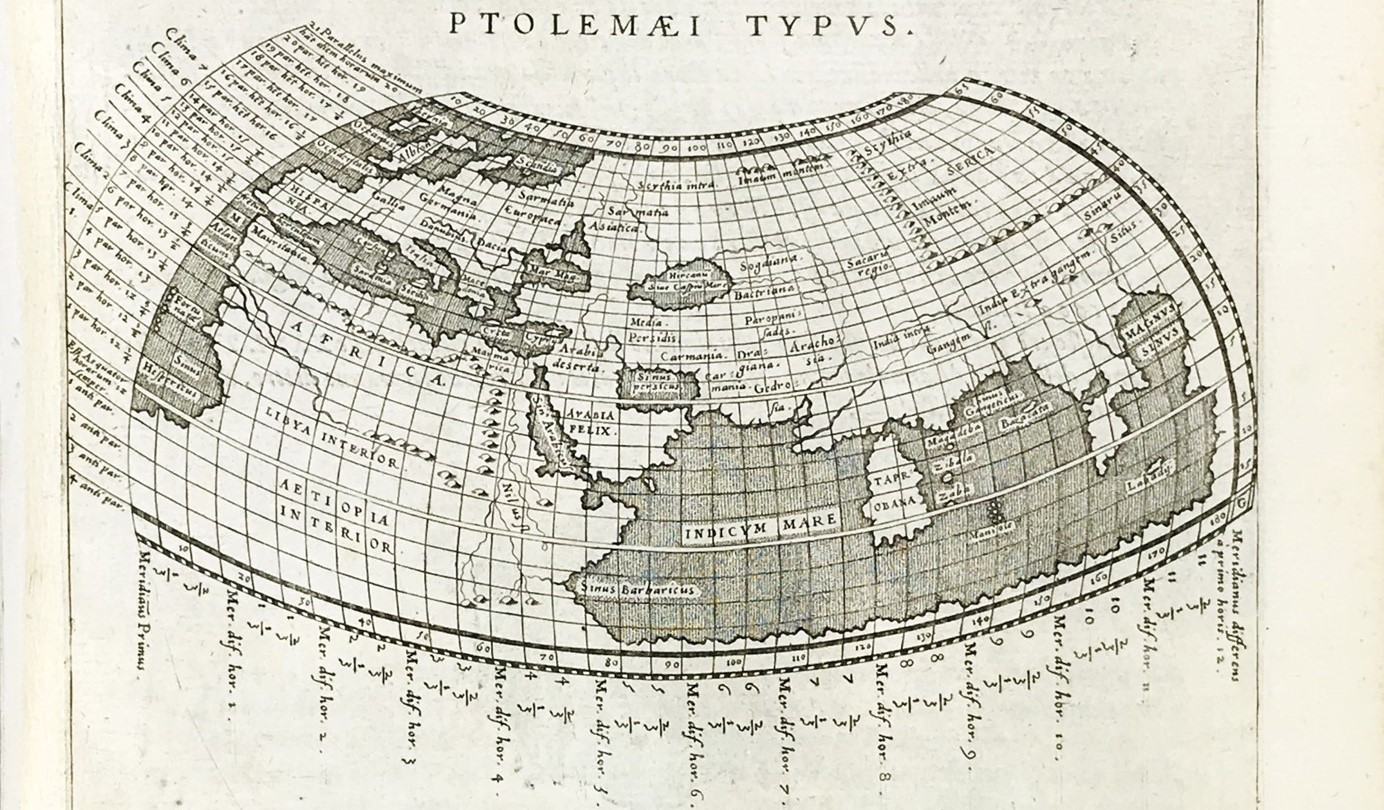 10th April 2024Rare Books, Prints, Autograph and Documents.Lot 64. PTOLEMAEUS. Geografia cioè descrittione universale della terra partita. 1597-98
10th April 2024Rare Books, Prints, Autograph and Documents.Lot 64. PTOLEMAEUS. Geografia cioè descrittione universale della terra partita. 1597-98 -
 10th April 2024Rare Books, Prints, Autographs and Documents.Lot 40. RONDELET. Libri de Piscibus Marinis. Lyon, Mathias Bonhomme, 1554
10th April 2024Rare Books, Prints, Autographs and Documents.Lot 40. RONDELET. Libri de Piscibus Marinis. Lyon, Mathias Bonhomme, 1554 -
 10th April 2024Rare Books, Prints, Autograph and Documents.Lot 183. FAUJAS DE SAINT-FOND. Recherches sur les volcans. 1778
10th April 2024Rare Books, Prints, Autograph and Documents.Lot 183. FAUJAS DE SAINT-FOND. Recherches sur les volcans. 1778 -
 10th April 2024Rare Books, Prints, Autographs and Documents.Lot 251. VOLTAIRE. Oeuvres complètes. Paris, Renouard, Edition de Kehl, 1819-1825
10th April 2024Rare Books, Prints, Autographs and Documents.Lot 251. VOLTAIRE. Oeuvres complètes. Paris, Renouard, Edition de Kehl, 1819-1825
Auction calendar
wed 10 April 2024
Bado and Mart Auctions is pleased to present the 2024 Spring Auction to be held on 10 April at 15.00 CET.
The auction consists [..]
Via dei Soncin, 28
35122 Padua
Italy
EXHIBITION: 5-7 April 2024 on appointment only.
To book your appointment, call 0039 049 8755317 or send an email to info@badoemart.it
We remind you that our staff remains at your disposal to carry out detailed condition reports with additional photos in addition to the pictures already present in the catalog.